Привіт! Мене звати Сергій Пащенко, я Data Engineer в NIX та спікер IT-конференції NIX Multiconf. Я великий фанат машинного навчання, Data Science і дата-інженерії в цілому. Сьогодні для мене вже очевидно, що майбутнє саме за квантовими обчисленнями.
Я переконаний: саме квантові комп’ютери демонструють потенціал, здатний вивести людство на новий рівень життя.
Щоб більш предметно поговорити про це, спершу варто згадати квантову теорію. Багатьом не подобаються складні математичні викладки, але без цієї бази ніяк. Квантові та класичні операції відрізняються. Для їх порівняння у цій статті я покажу приклади розв’язання класичних задач на традиційному та квантовому комп’ютерах. Також торкнемося квантового обчислення з боку прикладного значення.
Квантовий світ вже поруч із нами
Комусь може здатися, що квантові комп’ютери і все пов’язане з ними — це десь далеко і не скоро, щось із фантастичних фільмів, але це не так. Квантовий світ вже давно поруч із нами. Причому йдеться не лише про теоретичні дослідження.
Квантові обчислення набувають усе більшої популярності в бізнесі, оборонному секторі та інших сферах:
- Автовиробник Hyundai Motor Company та компанія IonQ оголосили про новий проєкт у галузі квантового машинного навчання. Суть у тому, що системи покращуватимуть навички розпізнавання дорожніх знаків та 3D-об’єктів на дорозі. Завдяки швидкості таких обчислень це стане в нагоді автономним транспортним засобам.
- Інший приклад — підписання угоди між Boehringer Ingelheim, найбільшою у світі приватною фармацевтичною компанією, та підрозділом Google Quantum AI. Команди планують створити R&D-центр, який моделюватиме молекулярну динаміку за допомогою квантових обчислень. Це дозволить прискорити й оптимізувати запуск на ринку нових препаратів.
- Цього ж року у НАТО повідомили, що проводять тестування захисту від кібератак із використанням квантових обчислень. На думку дослідників, такі комп’ютери зможуть швидко знаходити ключі до поширених методів шифрування даних. Тому вже сьогодні треба шукати нові варіанти протидії хакерам.
Згідно прогнозу міжнародного аналітичного центру IDC, світовий ринок квантових обчислень продовжить стрімко зростати: з $412 млн у 2020 році — до $8,6 млрд вже у 2027-му.
Тобто приріст витрат на квантові обчислення як на послугу складатиме щонайменше 50% щороку. Перспективи вражають настільки, що варто розібратися в цій темі глибше.
Базові поняття для роботи з квантовими обчисленнями
Квантова перевага
Квантові комп’ютери є набагато потужнішими у порівнянні з класичними. Якщо перенести закон Мура на сучасну електроніку у вигляді відеокарт та центральних процесорів, то з кожним періодом технологічний процес розміщення транзисторів на підкладинці призводить до зменшення типового пакету та збільшення потужності обчислювальних пристроїв.
Але в мікро- і наноелектроніці людство вже підходить до розмірів транзисторів близько 2-3 нм. Якщо йти далі цим шляхом, на такому рівні класичні закони фізики перестануть працювати і почнуть діяти правила квантової механіки.
Одним із фундаментальних понять цієї частини фізики є квантова заплутаність.
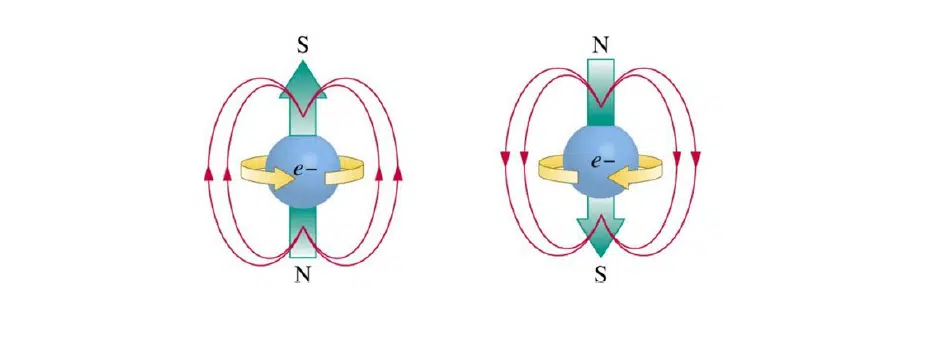
Квантова заплутаність говорить про те, що деякі частки квантового світу, від електронів до кварків і глюонів, можуть бути пов’язані між собою. Такі частки називають заплутаними. Якщо рознести їх у просторі та в однієї з них змінити спін або орієнтацію на протилежний, так само зміниться спін і в іншої заплутаної частинки.
Саме тут закладається розуміння того, як це можна використовувати з точки зору обчислювальної техніки.
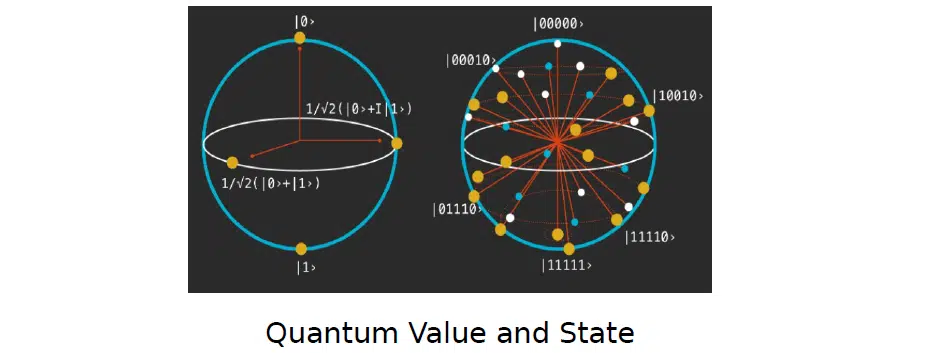
Ще одним з основних понять є квантове значення та квантовий стан. Давайте розберемо їхнє значення та особливості роботи з ними нижче:
Суперпозиція та квантова невизначеність
Суперпозиція випливає зі значення квантової заплутаності. Якщо у певній квантовій системі допустимі одразу два стани, то припустима і їхня довільна лінійна комбінація.
Я не буду вдаватися в деталі, це тема для окремої статті. Головне, що тут треба знати — саме цей закон квантової фізики використовується для побудови кубітів, квантових бітів та для операцій із ними.
Принцип суперпозиції проявляється в багатьох випадках, що доводить всім відомий кіт Шредінгера. В цьому експерименті розбирається принцип невизначеності.
Частинки квантового світу настільки маленькі і в той же час знаходяться у настільки великому об’ємі простору, що з точки зору детермінованої гіпотези неможливо чітко сказати, де знаходиться та чи інша з них. Іншими словами, кожна частинка одразу перебуває в одній точці і всюди.
Більше того, за копенгагенською інтерпретацією корпускулярно-хвильового дуалізму частка може вести себе і як частка (тобто окрема партіція), і як хвиля. Тому у нас вже існують інстанси, побудовані на різних принципах — на хвильовому та частковому.
Можливості квантових систем
Чому квантові комп’ютери та системи в цілому доволі складні? Проблема не лише в розмірах часток, якими вони оперують. Для більш-менш точного контролю квантового світу та проведення вимірів потрібно позбавитися від шуму, який з’являється через вплив на квантову систему теплової ентропії.
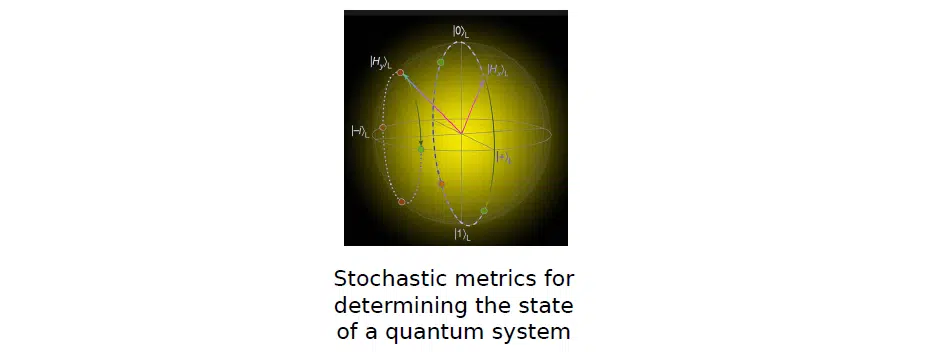
Через це для опису розподілу або щільності проходу хвильової функції в заданому коридорі або якоїсь частки використовують стохастичні метрики і теорію ймовірності. Все це є в процесі роботи самого квантового комп’ютера.
Наступне важливе поняття — це стохастична ініціалізація. До початку здійснення квантових обчислень потрібно проініціалізувати систему. Це робиться за допомогою рандомних чисел, які пізніше підлягають квантовій оптимізації. Однак ця ініціалізація впливає на квантовий світ та залежить від шуму навколишнього середовища. Тому мають бути не детерміновані розподіли метрик, а саме стохастичні.
Квантова система не може повернутися від значення до стану. Від початку вона знаходиться у стані суперпозиції. Але після здійснення виміру цього стану система переходить у детермінований порядок — і це вже є значення. Тому система не може повернутися до стану невизначеності. Це дуже принциповий елемент, пов’язаний із претрейном квантових моделей.
Варто ще згадати чутливість до шуму. Це один із найбільших наших ворогів, який сильно впливає на стан квантової системи. Для боротьби з ним розробники квантових комп’ютерів наділяють їх величезним рефрижератором, який працює на наднизьких температурах для нівелювання теплової ентропії. Хоча сам CPU у квантовій техніці доволі невеликий.
Значення проти стану
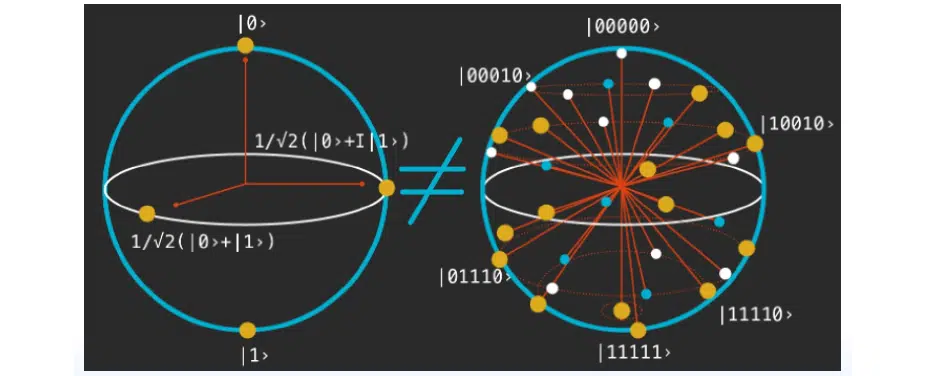
Під час ініціалізації ми не знаємо точно, яким чином проводимо її. Цей стан системи саме і називається станом. А після виміру кубіту або якоїсь іншої частки ми спостерігаємо, фіксуємо та отримуємо значення. Ці поняття не можна плутати через їх незворотність.
Зліва на малюнку зображені конкретні значення — фіксовані кубіти за деякими базисами. Вони не можуть бути повернені у рандомну стохастичну інтерпретацію квантової системи, як наведено справа:
Приклади класичних задач
MNIST Classification
Пропоную для прикладу розв’язати відому серед дата-саєнтистів задачу MNIST Classification. У ній є дата-сет із рукописних цифр з кількістю класів 10: від 0 до 9.
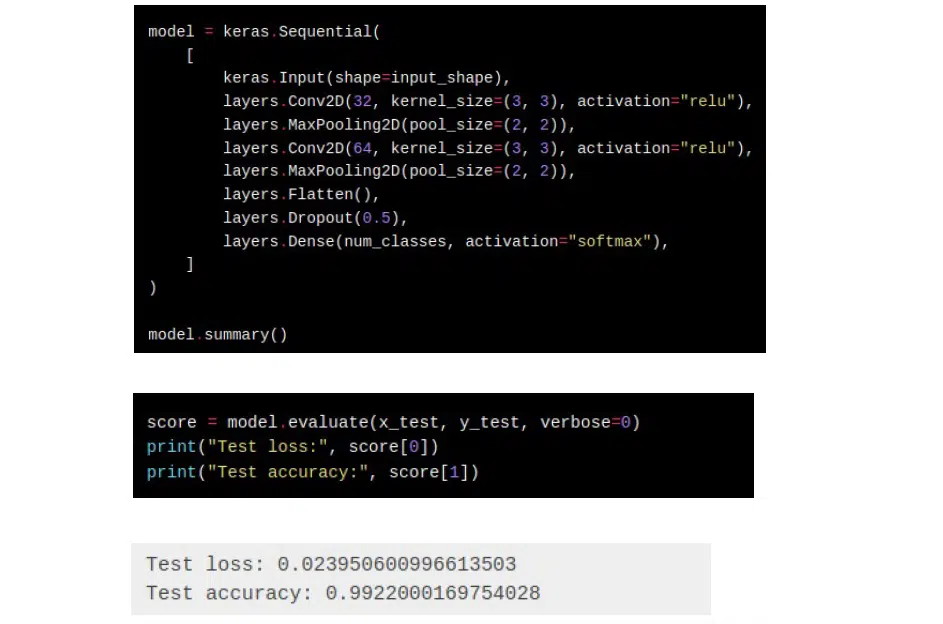
Для вирішення цієї задачі потрібна простенька модель, зроблена у коді нижче. Маємо деякий вхід та конвуляційні згорки, а класифікація йде просто на softmax. Точність на такому дата-сеті дуже висока — у нашому випадку 99,22%. Для досягнення статистичної потужності системи потрібно небагато епох.
У звичній інтерпретації це все працює зрозуміло. Модель, виходи та входи, леєри, вся математика та навіть дані представляються у вигляді бінарної інтерпретації. Тобто все закодовано у традиційну послідовність нулів та одиниць.
Квантові системи
Щоб зрозуміти спосіб розв’язання такої задачі з квантовою системою, треба передусім розібратися, що являє собою з точки зору математики кубіт та нотація бра-кет, також відома як нотація Дірака.
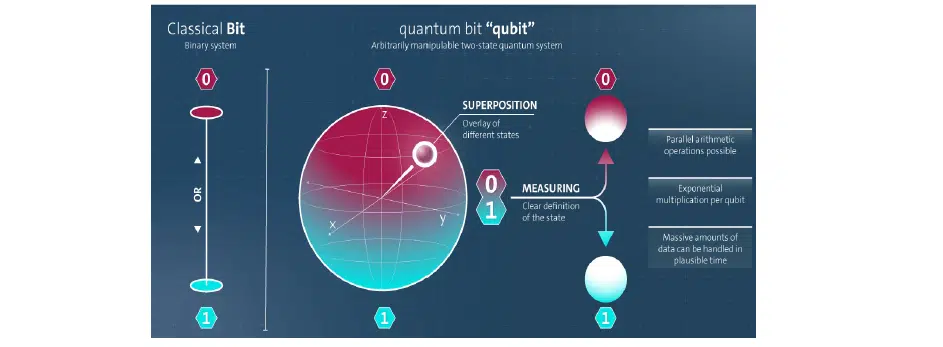
На ілюстрації зображені класичний біт та квантова інтерпретація, застосована на сфері Блоха:
Кубіт — це вектор комплекснозначних чисел. Переважна більшість перших квантових систем або комп’ютерів базувалася на лазерах. Для операцій ними потрібно керувати амплітудно-фазовими частотними характеристиками, які зі свого боку дуже добре описуються за допомогою саме комплекснозначних чисел. Тому коли Нільс Бор підтверджував гіпотези квантової механіки, ці математичні інструменти були вже достатньо відомими. Через це комплекснозначна інтерпретація суттєвим чином спрощує математичні викладки.
Узагальнена форма квантового біту записується так, як показано в лівій частині цього виразу:
Якщо потрібен кубіт цієї форми, розкладеної за базисом, треба застосувати формулу, як наведено справа. Все це виглядає доволі просто, як у лінійній алгебрі. Однак наголошу: в цьому прикладі комплекснозначних чисел немає, до них ми звернемося у наступній підтемі.
Квантові базиси та сфера Блоха
У класичній квантовій механіці виділяється декілька типів основоположних базисів: Z-базис, Y-базис та X-базис. Для квантових обчислень зазвичай використовується Z-базис. Він більш близький для сприйняття дата-саєнтистами і вченими, які працювали над задачами з оптимізації або з класичним машинним навчанням.
При проведенні вимірів на сфері Блоха буде простіше інтерпретувати значення кубіта, який ближче до 1 або до 0, ніж до деяких комплекснозначних чисел. Хоча це не виключає можливості використання Y- чи X-базисів. У деяких випадках їх застосування є зручнішим.
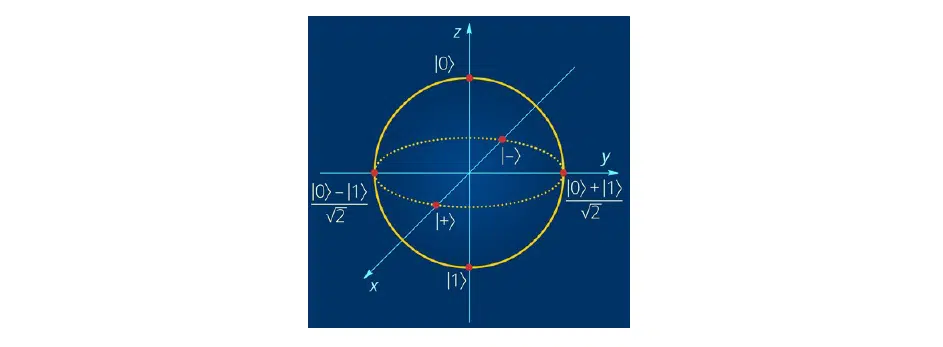
Щодо самої сфери Блоха, то це просто деяка інтерпретація розподілу кубітів у просторі. Базис мінус та плюс, який позначається у вигляді X, спрямований вздовж осі Х, Y-базис — осі Y, а Z-базис — відповідно до осі Z.
Квантові гейти та ротації
Коли ви розкладаєте кубіти у вигляді комплекснозначних чисел за деякими базисами, виникає питання: що з цим робити далі? Для проведення оптимізації потрібно варіювати деякі параметри квантової системи.
Тут стануть у нагоді квантові гейти — оператори, на базі яких будуються більш складні квантові схеми. Найбільш розповсюдженими операторами є гейт Адамара і T-gate. За теоремою інтерполяційної послідовності квантових схем будь-яка складна квантова система може бути редукована до послідовності саме цих гейтів:
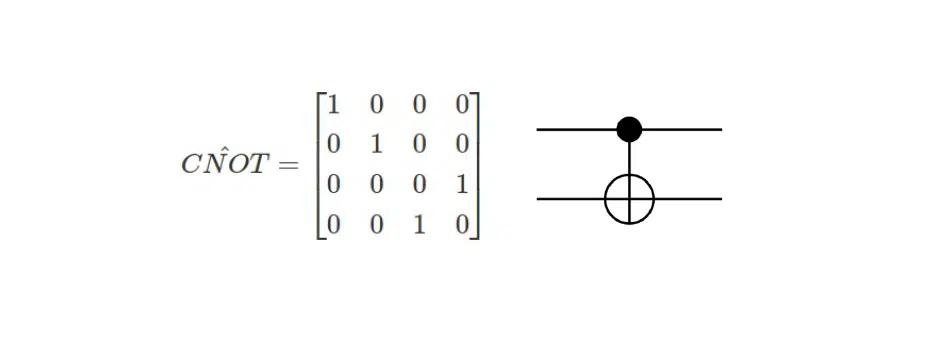
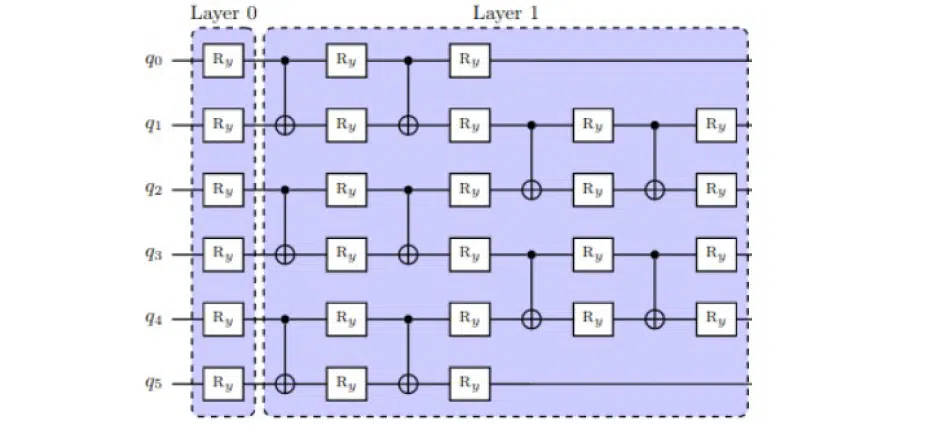
Також популярним є гейт CNOT, який інвертує один біт спостерігача та один контрольний біт. На схемі нижче можна побачити, як проініціалізувати квантову схему з цим оператором:
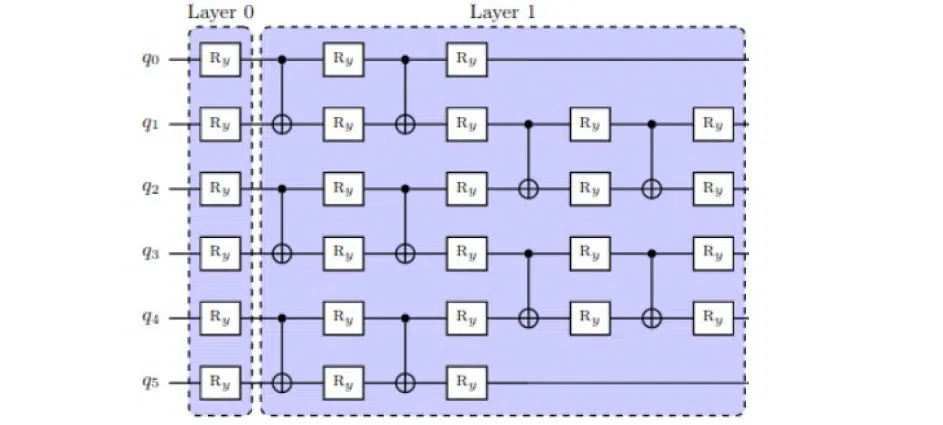
Замало задати біти та розібратися, як готуються квантові схеми. Для переходу від заплутаного значення квантової системи та здійснення виміру потрібно задати оператори Паулі (оператори виміру). Більш детально ознайомитися з ними можете в будь-якій квантовій теорії. Я ж обмежусь тим, що оператори Паулі являють собою основну концепцію з точки зору отримання або переводу квантової системи зі стану суперпозиції до стану значення.
Для зміни значення кубіта його потрібно крутити — проводити ротацію навколо сфери Блоха. Тому варто розглянути оператори RY, RX та RZ. Знову ж таки я не буду зосереджуватися на цьому. За бажання можете ознайомитися з цією теорією самостійно.
На вже згаданій схемі ми ініціалізуємо кубіт q0 та крутимо його навколо осі RY, тобто домножуємо на матрицю RY. Це дозволить йому змінити значення на сфері Блоха:
Чому саме ротація є ключем до знаходження оптимального значення стану квантової системи? При повороті кубітів вони будуть змінювати своє значення. Якщо побудувати замкнений цикл оптимізації, то можна зрозуміти, яке значення цієї частинки зробить квантову схему найбільш ефективною при розв’язання задачі:
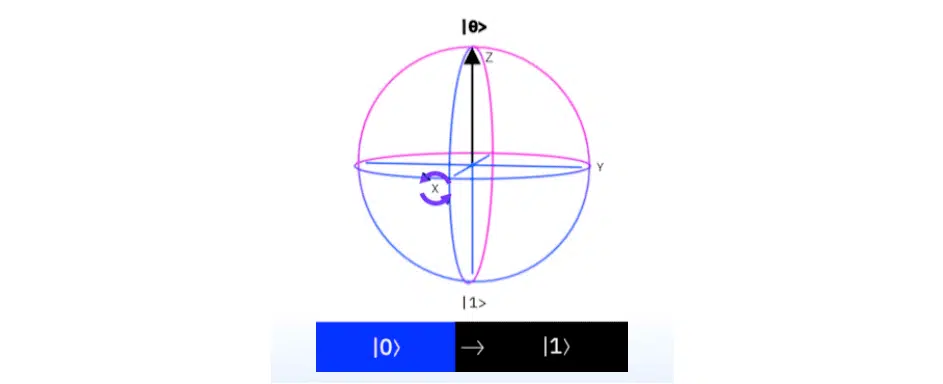
Але тут треба бути уважним. Якщо ініціювати кубіт і крутити навколо осі RX, то оператор Паулі має вимірювати значення частинки за віссю Z.
Чому? Якщо крутити проініціалізовані нулі, то значення Z змінюється повністю — від нульового до першого. Якщо ж крутити навколо осі Z та вимірювати за допомогою оператора Σ Z, тоді значення Z буде незмінним. Це може призвести до схоплювання квантового ембедінгу даних та взагалі моделі. Замість варіативної схеми ви отримаєте сміття з даних.
Читайте продовження моєї статті згодом на Highload. У ній я торкнуся квантових обчислень в машинному навчанні, розкажу про їх типи. А ще розглянемо фреймворки та хмарні платформи для запуску коду і розберемо реальний приклад на квантовому інстансі. Stay tuned!
Читайте також: Новий квантовий комп’ютер Amazon заснований на котах Шредінгера: у компанії розробили новий підхід до створення кубитів
Favbet Tech – це ІТ-компанія зі 100% українською ДНК, що створює досконалі сервіси для iGaming і Betting з використанням передових технологій та надає доступ до них. Favbet Tech розробляє інноваційне програмне забезпечення через складну багатокомпонентну платформу, яка здатна витримувати величезні навантаження та створювати унікальний досвід для гравців.
Цей матеріал – не редакційний, це – особиста думка його автора. Редакція може не поділяти цю думку.










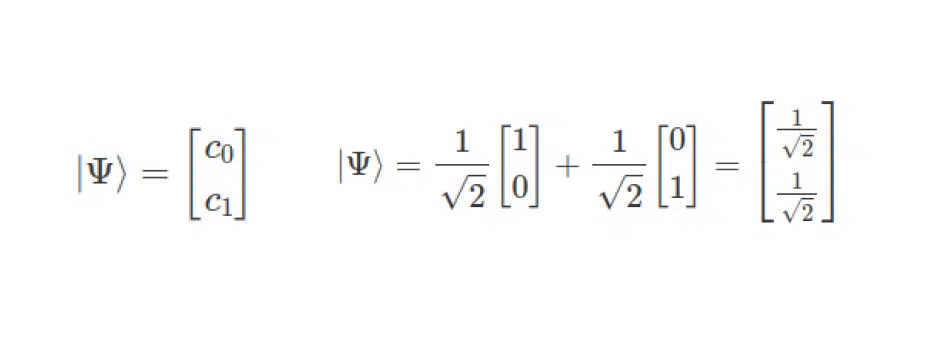
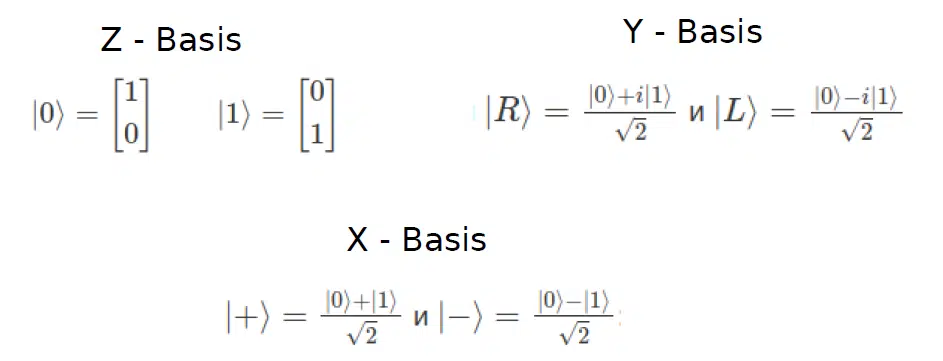
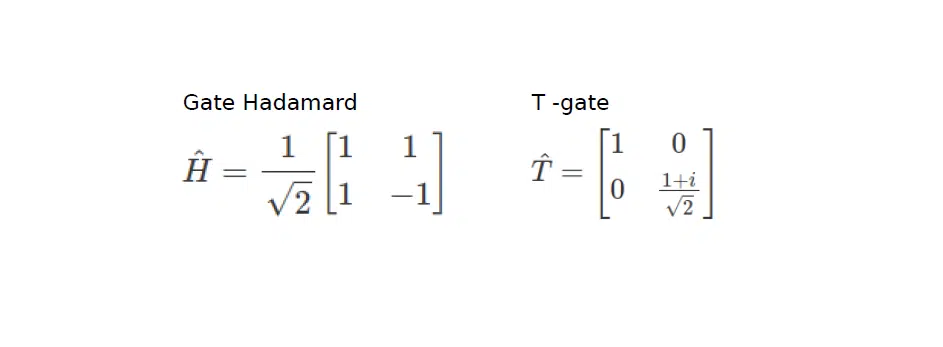
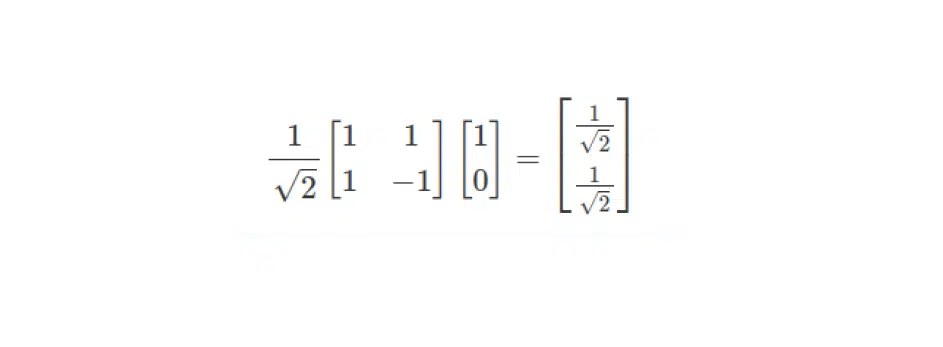
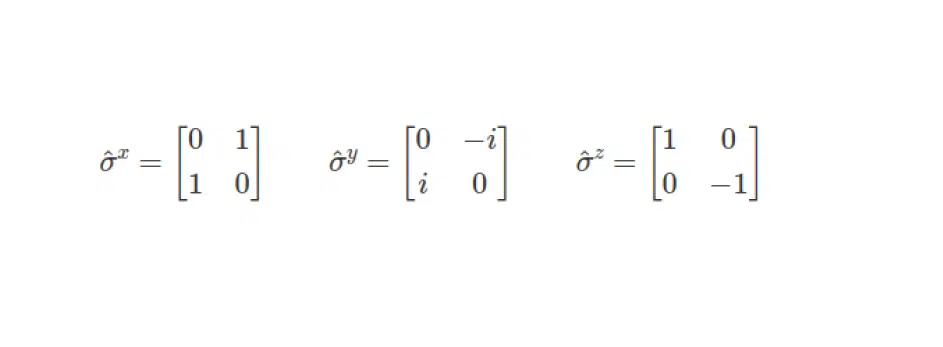
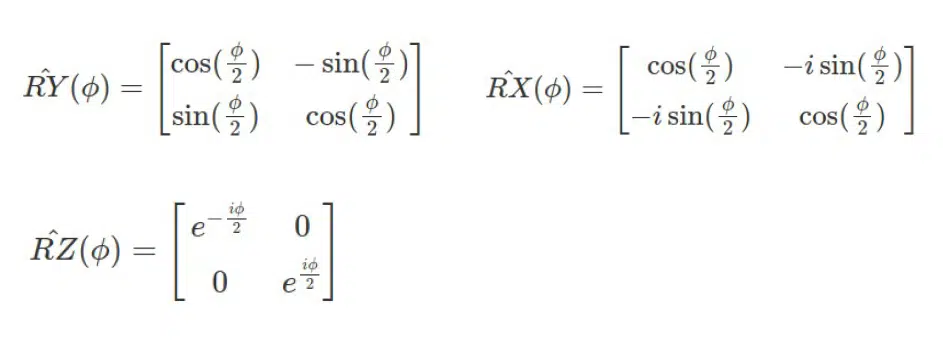












Сообщить об опечатке
Текст, который будет отправлен нашим редакторам: