Алгоритм Дейкстры в Java: шаги, визуализация и недостатки

Если объяснять коротко, то алгоритм Дейкстры — это алгоритм, который используется для определения кратчайшего пути от начального узла до всех остальных. Алгоритм называют жадным, потому что он всегда отмечает ближайшую вершину графа.

Алгоритм Дейкстры / baeldung.com

Графы в программировании — это удобный способ хранения определенных типов данных. Например, алгоритм может работать с числами или координатами, он может использоваться в приложениях для навигации и находить кратчайшие пути из пункта А в пункт В. Концепция графа была перенесена из математики и адаптирована под нужды информатики. В итоге обход графов стал обычной задачей, используемой в науке о данных и машинном обучении.

Шаги алгоритма

Вот список шагов, которые выполняет алгоритм Дейкстры:

• устанавливает расстояние до начального узла равным нулю;
• устанавливает расстояние до всех остальных вершин на бесконечное значение;
Онлайн-курс "Digital Marketing" від Laba.
Розширте пул навичок у роботі з аудиторією. Навчіться запускати рекламні кампанії без зайвих витрат бюджету з сучасними інструментами діджитал-маркетингу, включаючи AI. .
Детальніше про курс
• выбирает неотмеченную вершину графа, которая находится на наименьшем расстоянии от начального узла, и отмечает ее;
• рассчитывает расстояние до смежных вершин, выбирая наименьшее расстояние при каждой оценке;
• отмечает следующий узел;
• алгоритм действует по этому сценарию до тех пор, пока все вершины не будут отмечены.

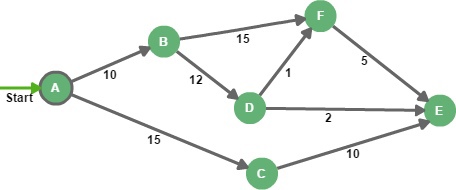
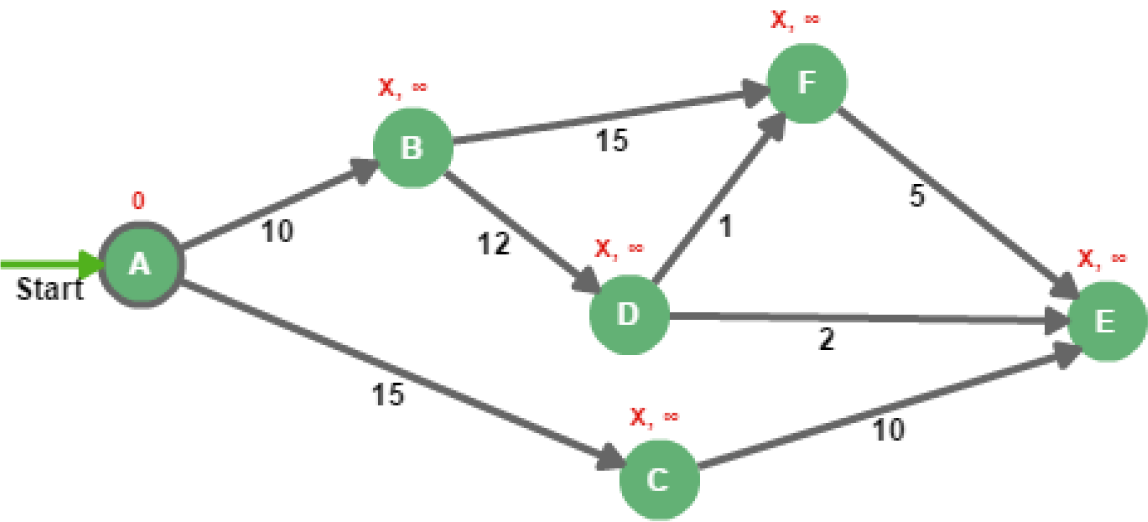
Визуализация работы алгоритма

На старте начальному узлу A присваивается значение 0, поскольку расстояние от вершины А до А равно 0.

На старте начальному узлу присваивается значение 0 / baeldung.com

Затем алгоритм оценивает расстояние до всех соседних узлов и ищет вершину с наименьшим расстоянием от изначальной точки.

Алгоритм ищет вершину с наименьшим расстоянием от старта / baeldung.com

Вершина A из неотмеченных переходит в отмеченные, а вершины B и C добавляются к списку неотмеченных,  потому что алгоритму еще предстоит оценить расстояние до них.

Теперь, когда есть соседние с А вершины B и С, алгоритм выбирает точку с наименьшим до нее расстоянием.

После того, как вершина будет обозначена как отмеченная, она становится отправной точкой следующего цикла. Когда будет найден кратчайший путь от стартовой точки до вершины, алгоритм начнет цикл поиска заново.

Эти этапы повторяются, пока все вершины в графе не будут отмечены.

Этапы повторяются, пока все вершины не будут отмечены / baeldung.com

Недостатки

Главный недостаток алгоритма в том, что его нельзя использовать для поиска кратчайшего расстояния в графах с отрицательными ребрами. Жадная стратегия алгоритма всегда выбирает отрицательное число в качестве меньшего расстояния.

Также из-за специфики жадного алгоритма на него уходит много времени и тратится много памяти программы. Поэтому некоторые специалисты предпочитают пользоваться алгоритмом A* для ускорения работы программы. А для работы с отрицательными числами применяется алгоритм Беллмана — Форда.

Код Java для алгоритма Дейкстры

Пример использования алгоритма в Java:

// Java implementation of Dijkstra's Algorithm
// using Priority Queue
import java.util.*;
public class DPQ {
    private int dist[];
    private Set<Integer> settled;
    private PriorityQueue<Node> pq;
    private int V; // Number of vertices
    List<List<Node> > adj;
 
    public DPQ(int V)
    {
        this.V = V;
        dist = new int[V];
        settled = new HashSet<Integer>();
        pq = new PriorityQueue<Node>(V, new Node());
    }
 
    // Function for Dijkstra's Algorithm
    public void dijkstra(List<List<Node> > adj, int src)
    {
        this.adj = adj;
 
        for (int i = 0; i < V; i++)
            dist[i] = Integer.MAX_VALUE;
 
        // Add source node to the priority queue
        pq.add(new Node(src, 0));
 
        // Distance to the source is 0
        dist[src] = 0;
        while (settled.size() != V) {
             //when the priority queue is empty, return
             if(pq.isEmpty())
               return ;
            // remove the minimum distance node
            // from the priority queue
            int u = pq.remove().node;
 
            // adding the node whose distance is
            // finalized
            settled.add(u);
 
            e_Neighbours(u);
        }
    }
 
    // Function to process all the neighbours
    // of the passed node
    private void e_Neighbours(int u)
    {
        int edgeDistance = -1;
        int newDistance = -1;
 
        // All the neighbors of v
        for (int i = 0; i < adj.get(u).size(); i++) {
            Node v = adj.get(u).get(i);
 
            // If current node hasn't already been processed
            if (!settled.contains(v.node)) {
                edgeDistance = v.cost;
                newDistance = dist[u] + edgeDistance;
 
                // If new distance is cheaper in cost
                if (newDistance < dist[v.node])
                    dist[v.node] = newDistance;
 
                // Add the current node to the queue
                pq.add(new Node(v.node, dist[v.node]));
            }
        }
    }
 
    // Driver code
    public static void main(String arg[])
    {
        int V = 5;
        int source = 0;
 
        // Adjacency list representation of the
        // connected edges
        List<List<Node> > adj = new ArrayList<List<Node> >();
 
        // Initialize list for every node
        for (int i = 0; i < V; i++) {
            List<Node> item = new ArrayList<Node>();
            adj.add(item);
        }
 
        // Inputs for the DPQ graph
        adj.get(0).add(new Node(1, 9));
        adj.get(0).add(new Node(2, 6));
        adj.get(0).add(new Node(3, 5));
        adj.get(0).add(new Node(4, 3));
 
        adj.get(2).add(new Node(1, 2));
        adj.get(2).add(new Node(3, 4));
 
        // Calculate the single source shortest path
        DPQ dpq = new DPQ(V);
        dpq.dijkstra(adj, source);
 
        // Print the shortest path to all the nodes
        // from the source node
        System.out.println("The shorted path from node :");
        for (int i = 0; i < dpq.dist.length; i++)
            System.out.println(source + " to " + i + " is "
                               + dpq.dist[i]);
    }
}
 
// Class to represent a node in the graph
class Node implements Comparator<Node> {
    public int node;
    public int cost;
 
    public Node()
    {
    }
 
    public Node(int node, int cost)
    {
        this.node = node;
        this.cost = cost;
    }
 
    @Override
    public int compare(Node node1, Node node2)
    {
        if (node1.cost < node2.cost)
            return -1;
        if (node1.cost > node2.cost)
            return 1;
        return 0;
    }
}

Результат применения алгоритма:

The shorted path from node :

0 to 0 is 0

0 to 1 is 8

0 to 2 is 6

0 to 3 is 5

0 to 4 is 3